1. Properties Of The Binary Operators Ûp And Ðown

1.1. Previous Definitions Of Ûp & Ðown

All good miners need to know their tools - what they are capable of and where they shouldn't be used. The same is true of Ûp and Ðown

Here is my definition for the binary operators "Ûp" and "Ðown"

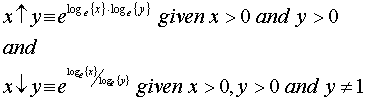...(1)

Here is my definition for the unitary operator "Ûp to the power of n" i.e.

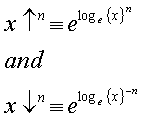...(2)

And here is my definition for the "Ûp Absolute" value of x - I think I'll call this the Ûpsolute value of x.

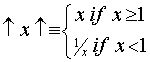...(3)

2. List of Properties For Up & Down

2.1 Commutative Property of Ûp & Ðown

...(4)

2.2 Associative Property of Ûp & Ðown

There are two possible combinations for the associative rule

..........................(5 a)

.........(5 b)

2.4 Distributive Property Of Ûp & Ðown

There are four possible combinations for the distributive rule

....(6 a)

...(6 b)

....(6 c)

...(6 d)

2.8 The Existence Of An Identity "e"

...(7)

2.9 The Existence Of An Inverse

...(8)

2.10 The Exponent Rules For The Up-Exponent (An "Uponent" perhaps?)

There are three possible exponent rules

.......(9 a)

...............(9 b)

....(9 c)

Here is a link to see some proofs on these group properties Appendix

3. Complex Ûp and Ðown

We realize from the definition of that

....(10) for all real values of x.

This is analogous to the familiar result that . However people "invented" a number j such that j ² = -1. I see no reason why I can't do the the same with the Ûp-Exponent. I will therefore define a new number p such that

...(11)

If j is called an "imaginary number" I think I'll call p a "phantasy number".

All p has to do is remain consistent within the rules of mathematics to exist, but if it behaves in any way odd or different to other numbers then it may indeed be a new number.

While I'm at it, I don't see why my "phantasy number" can't be paired up with conventional numbers in a similar fashion to z = x + j · y. I therefore propose a combination number w defined as

...(12)

If "z" is called a "complex number" I think I'll call w a "profound number"

4. Summary for Ûp and Ðown

In this web chapter I have listed the group properties of Ûp and Ðown . I have included the Ûp-Exponent or "Ûponent" properties and the "Ûpsolute value" definition, analogous to the absolute value

I have also proposed the possible existence of a phantasy number p in analogous definition the the imaginary number j. Just as complex numbers z are constructed from a real and an imaginary part, I have proposed a profound numbers w constructed from a real and a phantasy part.

No rules of arithmetic have been transgressed at this stage, nor have the definition for phantasy and profound numbers followed any different reasoning or allowances than those afforded to imaginary and complex numbers.

So I think all's fair in maths and conjecture!

Return To: Inventing Numbers

or Conjecturals

or Ian Scotts Technology Pages