The intention of this approach is to train the Neural Network (NN) on a group of lessons as opposed to training on one question-answer (QA) at a time (as in competitive training). This should remove the "bias" that prefers the first and last few QAs exhibited by competitive training (as we also tend to exhibit). Although this biological similarity may be of advantage if we wish to emulate biological behavior in a (silicon or other semiconductor) based machine, my intention is use potentially useful biological characteristics and architectures to make a silicon machine, but only for the purpose of creating useful behavior.
The disadvantage of competitive learning is that each new QA disrupts previous learning and therefore must increase overall training time and compromise learning effectiveness. A consensus approach uses all QAs in a lesson group to produce an overall learning performance error ê. The NN weights are then modified in an attempt to reduce this total performance error ê. In this way, no particular QA is advantaged at least statistically speaking (although certain QA's will perform better than others).
Note: I will use MathCAD to demonstrate the method (MATHCAD8) but it is timely to identify some of MathCAD's "quirks". Although MathCAD has an excellent user interface it is interpretive (slow) rather than compiled (faster) and this usability feature may have caused some unexpected anomalies in its operation.
Matrix operation in particular are limited in dimension (not size). For example Wm,n represents a two dimension matrix (square-rectangle) and these operations are fine. However Wm,n,p should represent a three dimension matrix (cube, etc) but not in a pure mathematical sense. Wm,n,p,q,... should represent higher dimensional matrices but these result in immediate error.
MathCAD treats three dimensional matrices as rows of two dimensional matrices but not as columns of two dimensional matrices (this causes immediate error). Also, this three D pseudo matrix cannot be directly operated on. Each 2 D matrix has the be extracted for operations and then returned.
For example let wm,n represent a 2D matrix. Wp = wm,n (some integer p) is supported as an operation but W<p> = wm,n will fail.
Further, if the 3 D composite matrix is saved to disk, it may not retrieve correctly.
MathCAD is usually tolerant of local errors and the program will "run around them" - a nice feature. However it will generate "internal error" with 3 D matrices and "programming" functions. This sometimes crashes the program, usually for no obvious reason (it may take 1000 iterations or 20 for example - extremely random).
External functions can be defined and used inside a "programming loop" but if these functions contain an if-then conditional statement, this can also cause an unexpected error.
I mention this as a caution only. If the quirks are known they can usually be worked around.
The use of a Least Squares Estimate for ê seems reasonable. Let us define the error per lesson to be,
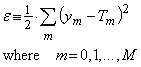...(1)
Equation (1) produces an error based on the sum of the squares of differences between each NN output node ym and the required Target value Tm for a NN with N+1 output nodes. For competitive training the error would be minimized for lesson 1, then for lesson 2 and so on, then the sequence would be repeated. The consensus approach produces a total error based on the sum of all errors produced for each kth lesson,
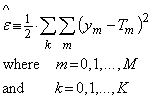...(2)
In this definition there are K+1 lessons of QAs presented to the NN and the total error is calculated.
Let us first define a suitable Non Linear Transform (NLT) that represents the input - output transfer function for each NN node (e.g. neuron in a biological system)
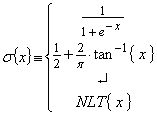...(3)
It is important to note that a purely linear transfer function will NOT work. Suitable NLTs include the sigmoid function, the inverse tangent function or other arbitrary functions "NLT" (may be piecewise defined). Now consider an input vector x presented to the NN. These are "scaled" by connecting weights w (axioms in a biological system) to present inputs to each "hidden layer" node immediately following the input layer. These hidden layer nodes then produce outputs based on their NLT.
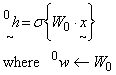...(4)
Note: The notation used shows W0 as a 3 D matrix where it's first row "0" contains the first weight matrix w. The upper left hand indices represent the first, second, third hidden layers, etc (0h, 1h, ... etc).
The second hidden layer nodes will then produce outputs given by,
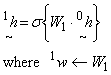...(5)
The number of hidden layer nodes must be one or greater. If a single hidden later NN is considered, then 1h represents the NN output y. In general a multiple hidden layer NN has an output y given by
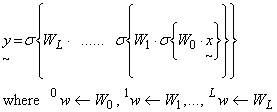...(6)
Equation (6) represents a "nested operation" from the first hidden layer 0h, followed by the second hidden layer 1h, continuing to the final hidden layer Lh and terminating at the output node layer y. Each inter-layer 2 D weight matrix pw is contained in the composite 3 D matrix Wp . (i.e. W is just a "storage" cell for each independent weight matrix wm,n ).
Note: This notation represents L+2 NN layers where L >= 1. Therefore the number of weight matrices is one less i.e. L+1. The final output y represents (what would have been defined as) L+2h.
Return To Artificial Intelligence
or to Ian Scotts Technology Pages
© Ian R Scott 2007 - 2008